动手学深度学习 1
一、数据操作+预处理
N维数组
N维数组是机器学习和神经网络的主要数据结构
0-d 标量:一个数字
1-d 向量:一个特征向量
2-d 矩阵:一个样本-特征矩阵
3-d RGB图片(宽×高×通道)
4-d 一个RGB图片的批量(批量大小batch×宽×高×通道)
创建数组
需要:
形状
每个元素的数据类型
每个元素的值
访问元素
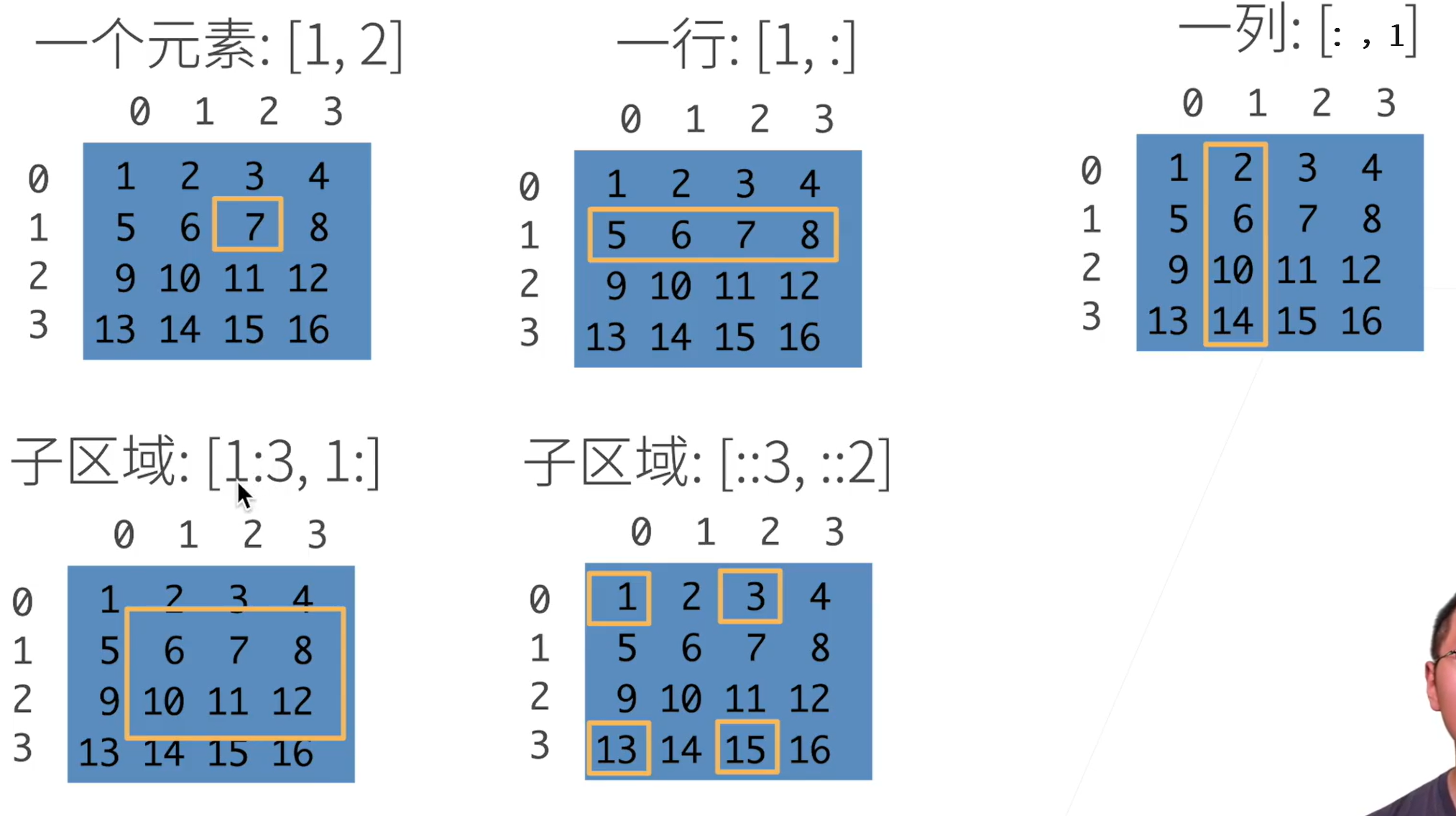
左下角子区域:1:3表示[1,3)
第二个子区域: ::3表示行是每3行一跳
::2表示列是每两列一跳
关于内存
x += y 就是直接在原来的x上加上y,与加法的形式不一样
x = x + y 本质上是将值给了一个新的x,开辟了个新的内存
矩阵乘法
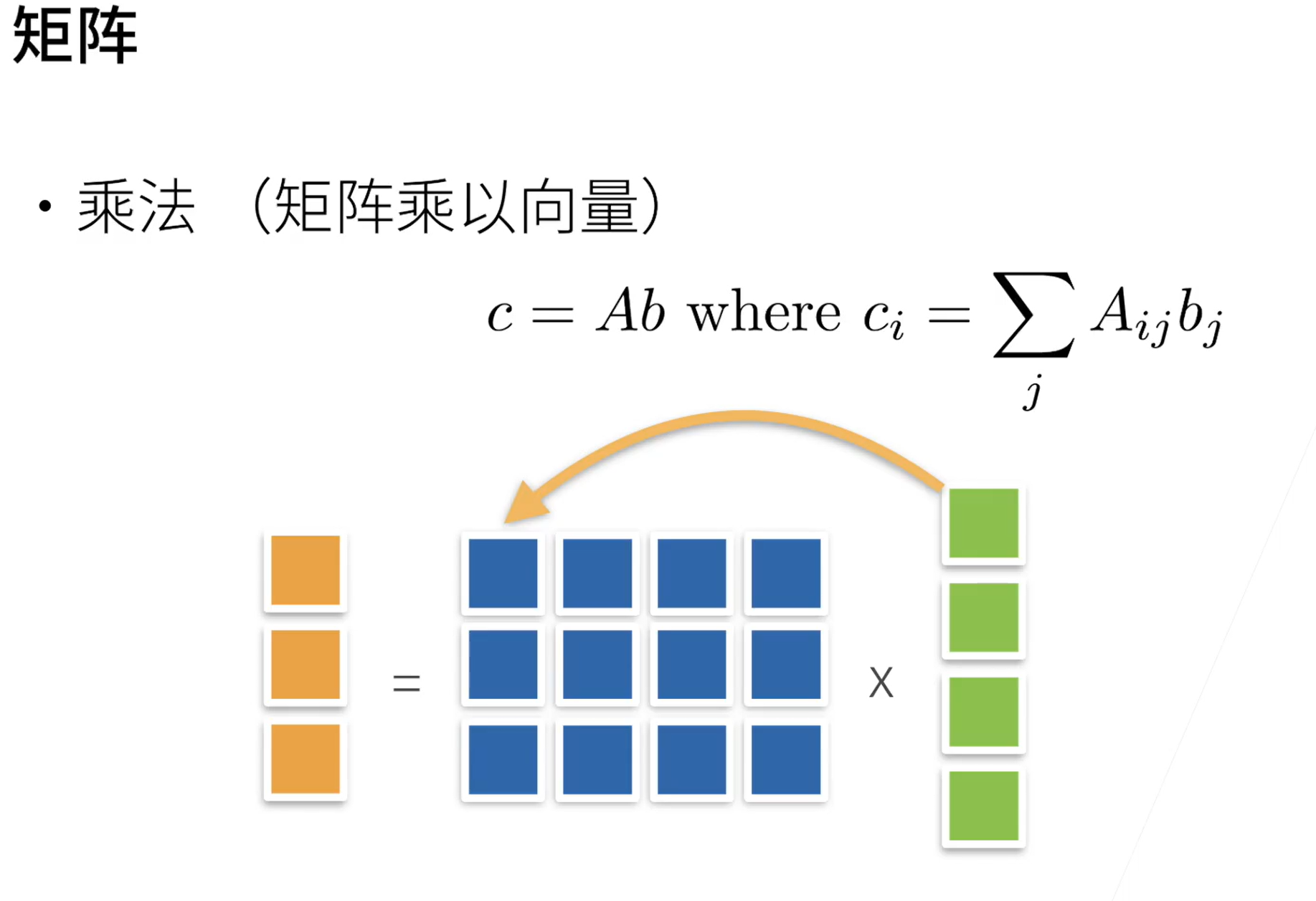
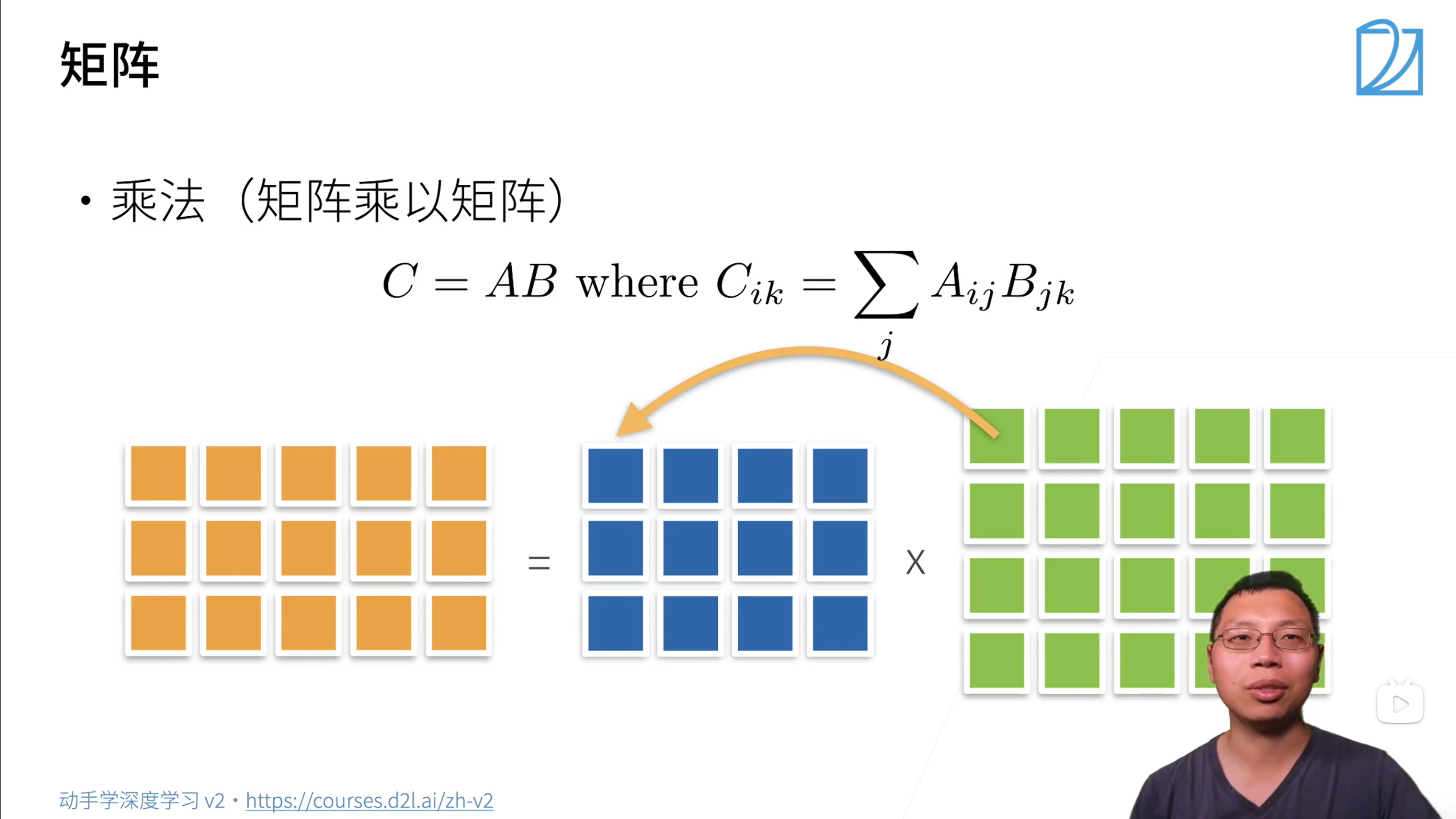
特征向量:不被矩阵改变方向的向量
矩阵范数的求法:
矩阵按列求和
axis=0 行
axis=1 列
就是照着那个轴拍扁(全相加)
按单个axis求和
比如shape [5,4]
axis = 1 ,sum:[5] 我不要列了–> 按列向右拍扁
按多个axis求和
shape [2,5,4]
axis=[1,2] sum:[2]
如果 keepdims=True 那对应的那个维度就不拍扁
shape [2,5,4]
axis=1, sum:[2,1,4]
二、线性回归
是对n维输入的加权,外加偏差
$$
y=w_1x_1+w_2x_2+…+w_nx_n+b
$$
向量版本:y=<w,x>+b
可以看做单层神经网络
衡量预估质量 —— 平方损失 L2 Loss
$$
l = \frac{1}{2}(y-\hat{y})^2
$$
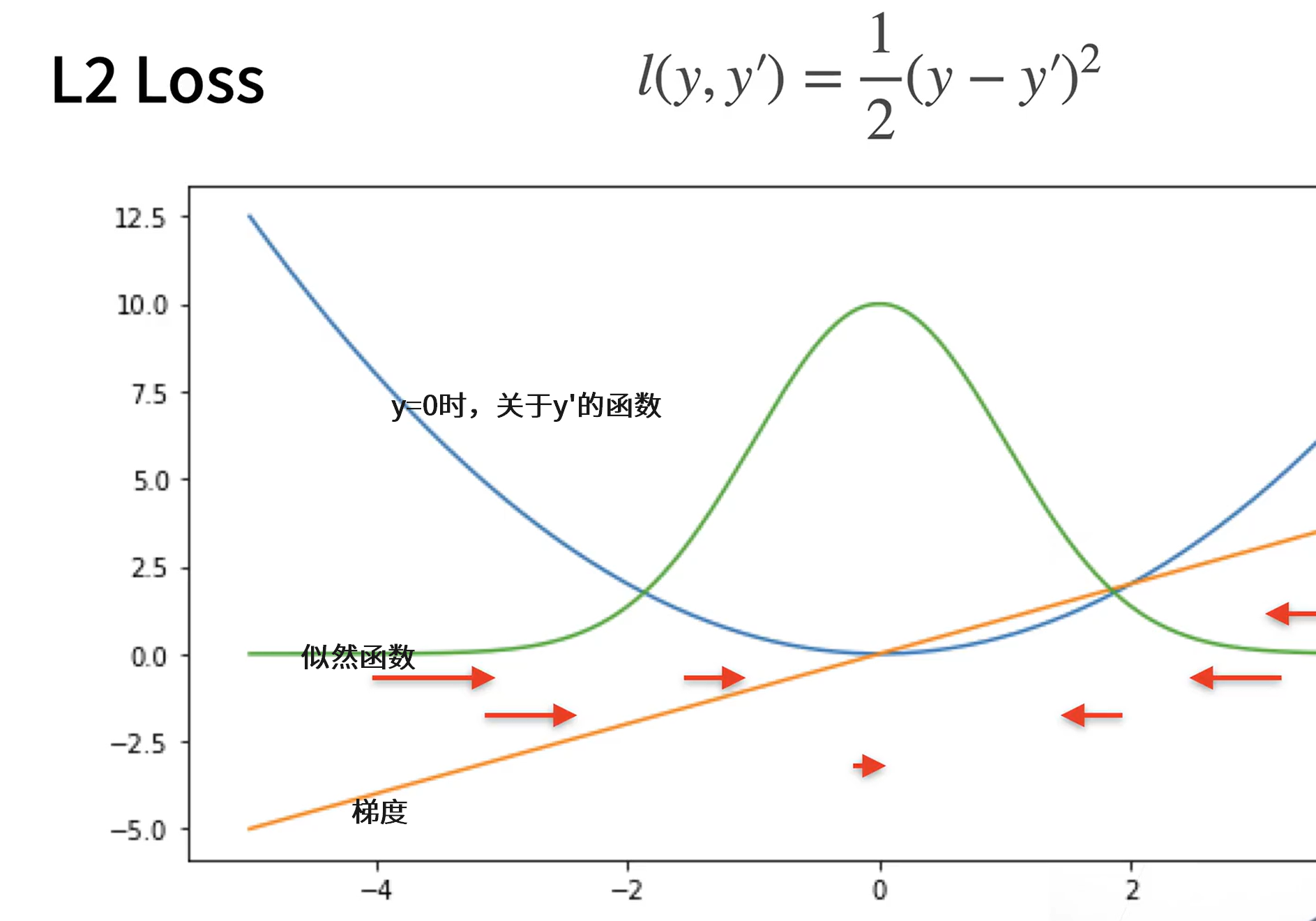
缺点:y‘和y相差很多时梯度太大 -》 使用L1 Loss
参数学习
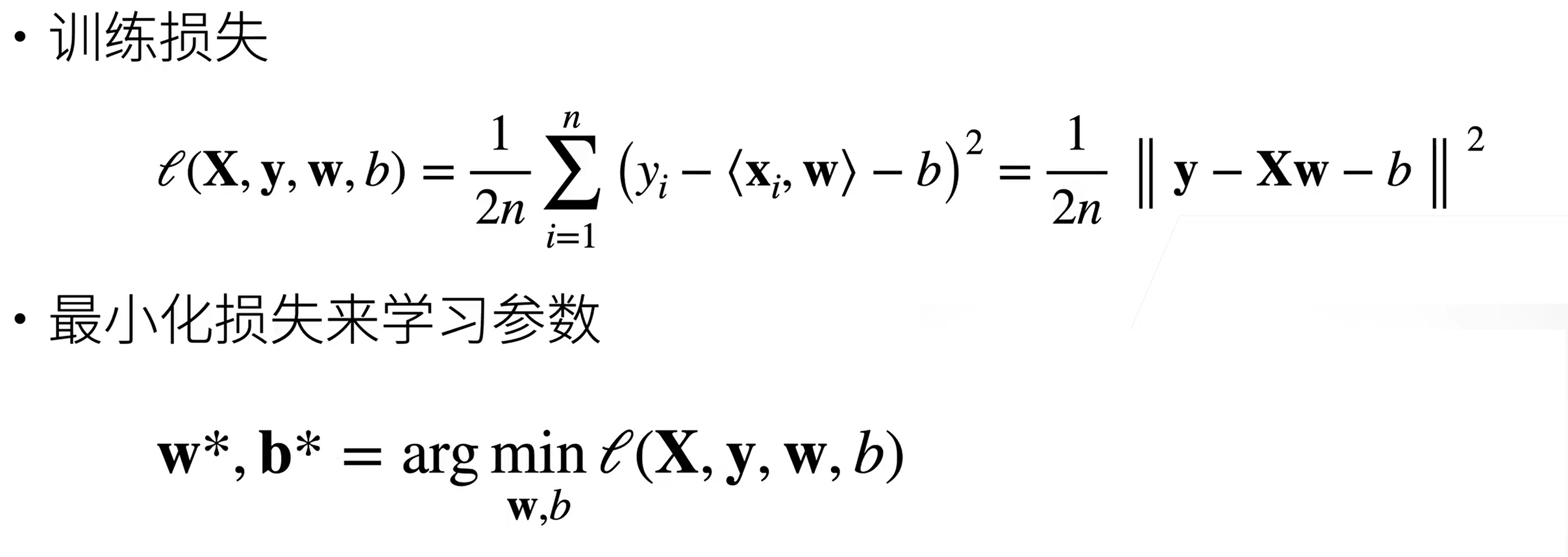
显示解
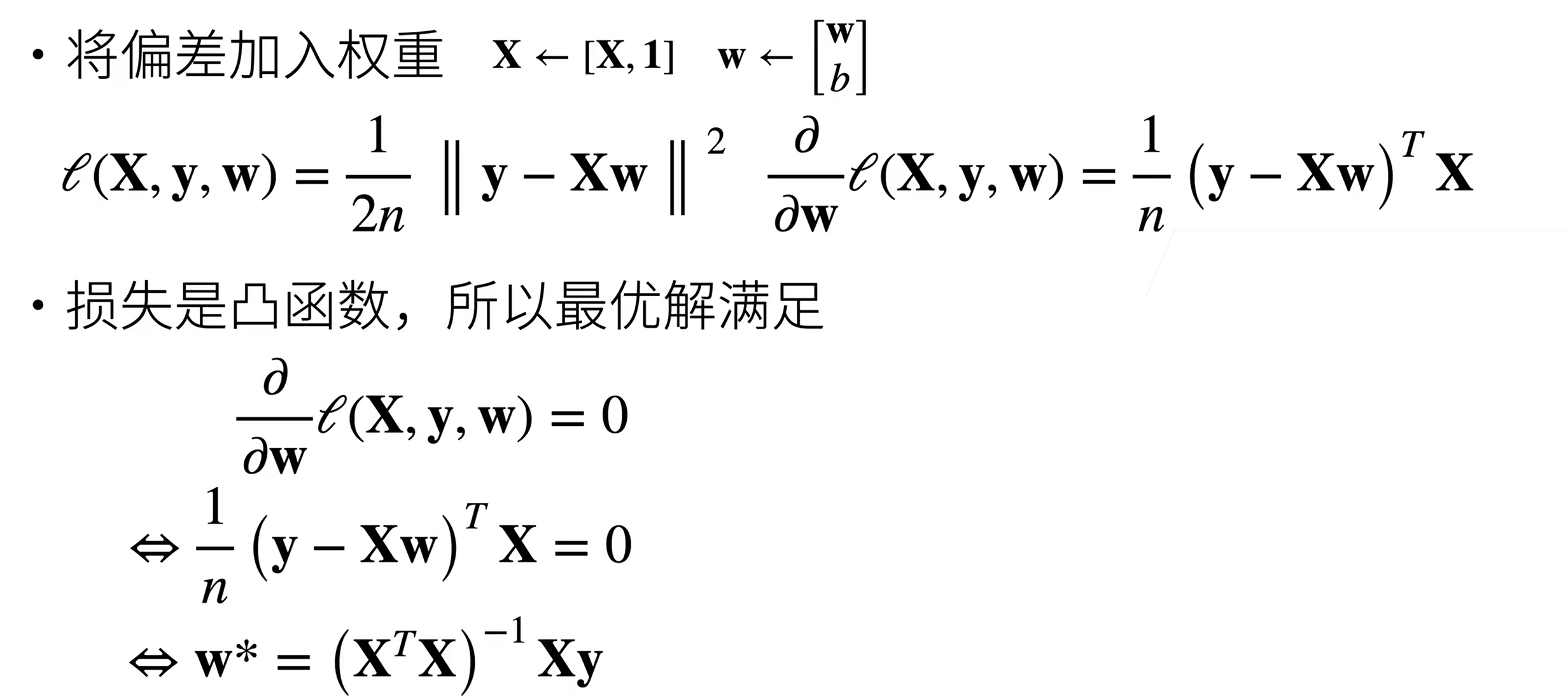
基础优化方法
梯度下降

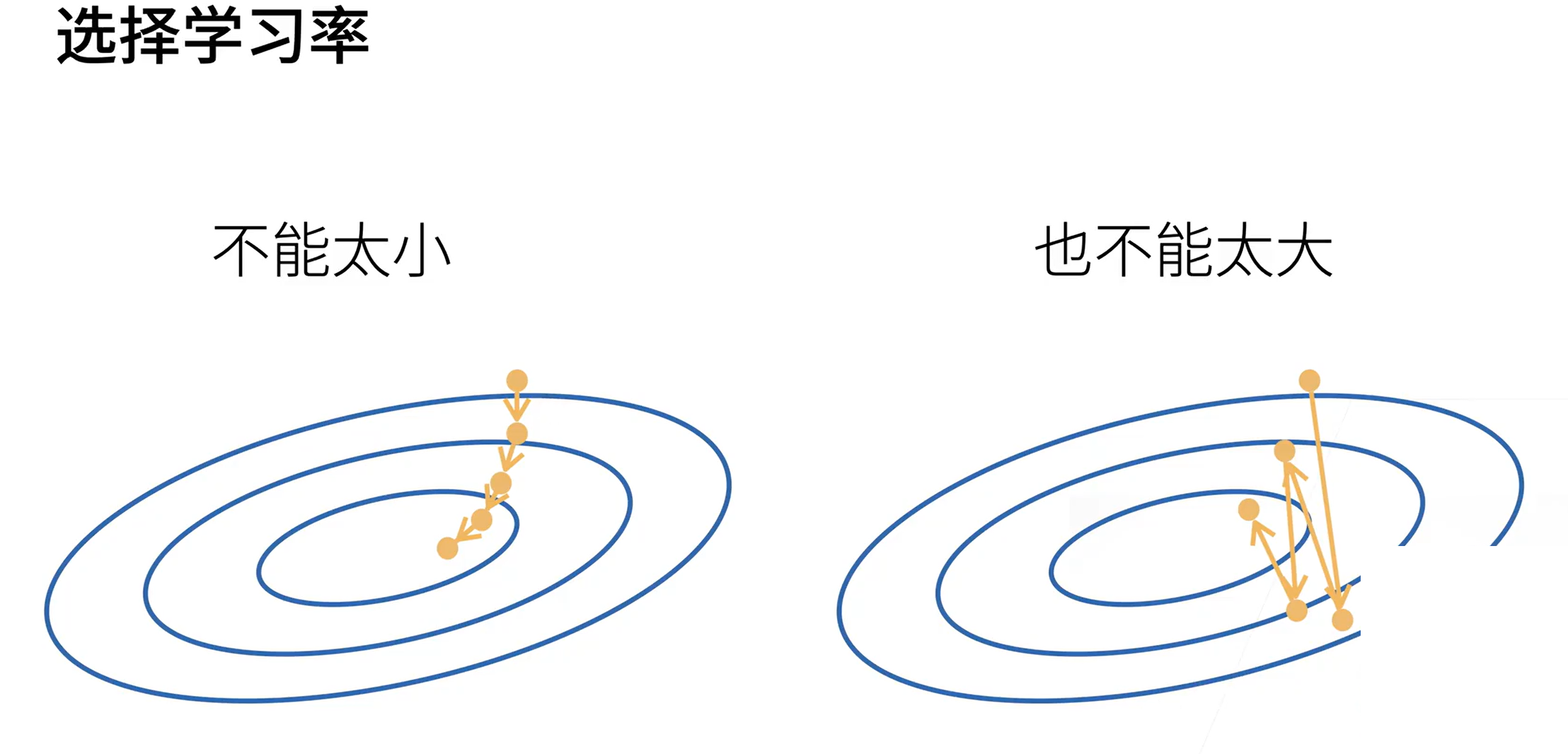
选择批量大小

batch_size 小的话可能会引入噪声,但这个噪声可能会使模型预测不走偏,因此准确度可能更高
随机梯度下降(SGD)
梯度下降是根据所有样本的平均损失进行计算,需要将所有样本重新计算一遍,非常浪费时间。
因此通常采用小批量随机梯度下降(SGD)进行求解。
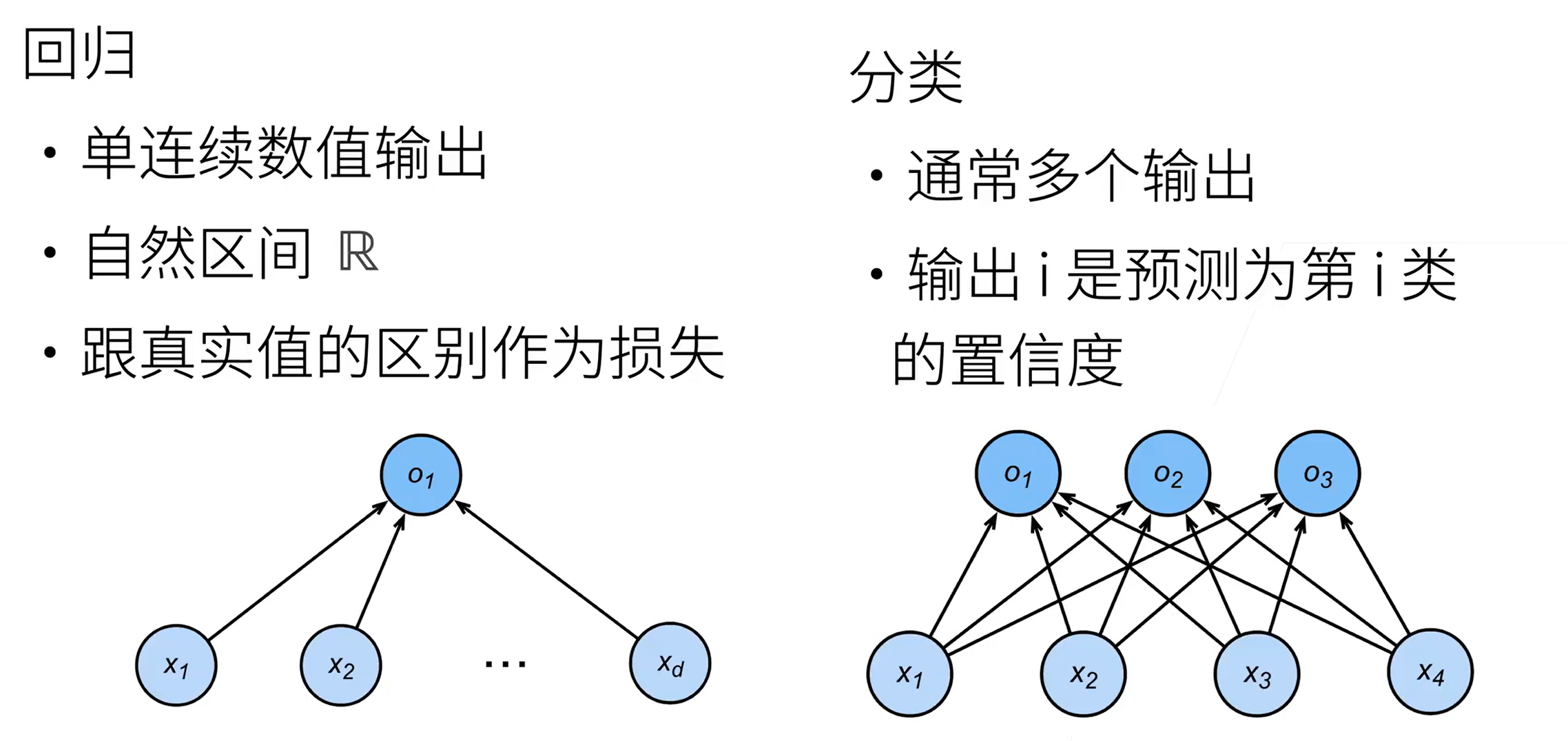
三、softmax 回归(多类分类模型)
得到每个类的预测置信度
使用交叉熵来衡量预测和真实情况的区别,作为损失函数
回归和分类的区别
无校验比例
希望预测出的类的置信度和别的类的置信度的差最大
校验比例
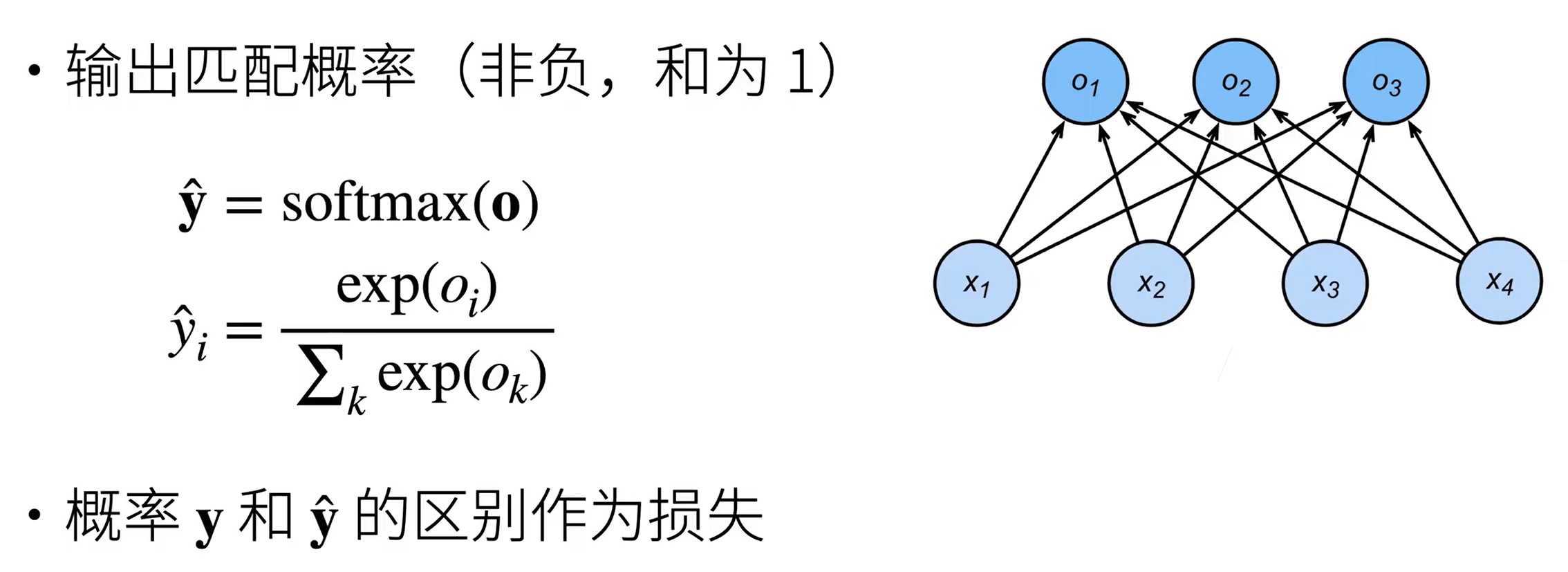
作指数是为了将数值变为非负。并且经过操作后使得加起来和为1
交叉熵损失
常用来衡量两个概率的区别
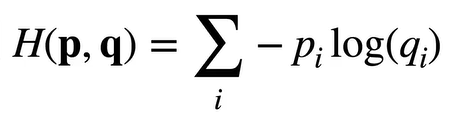

损失函数
L1 Loss
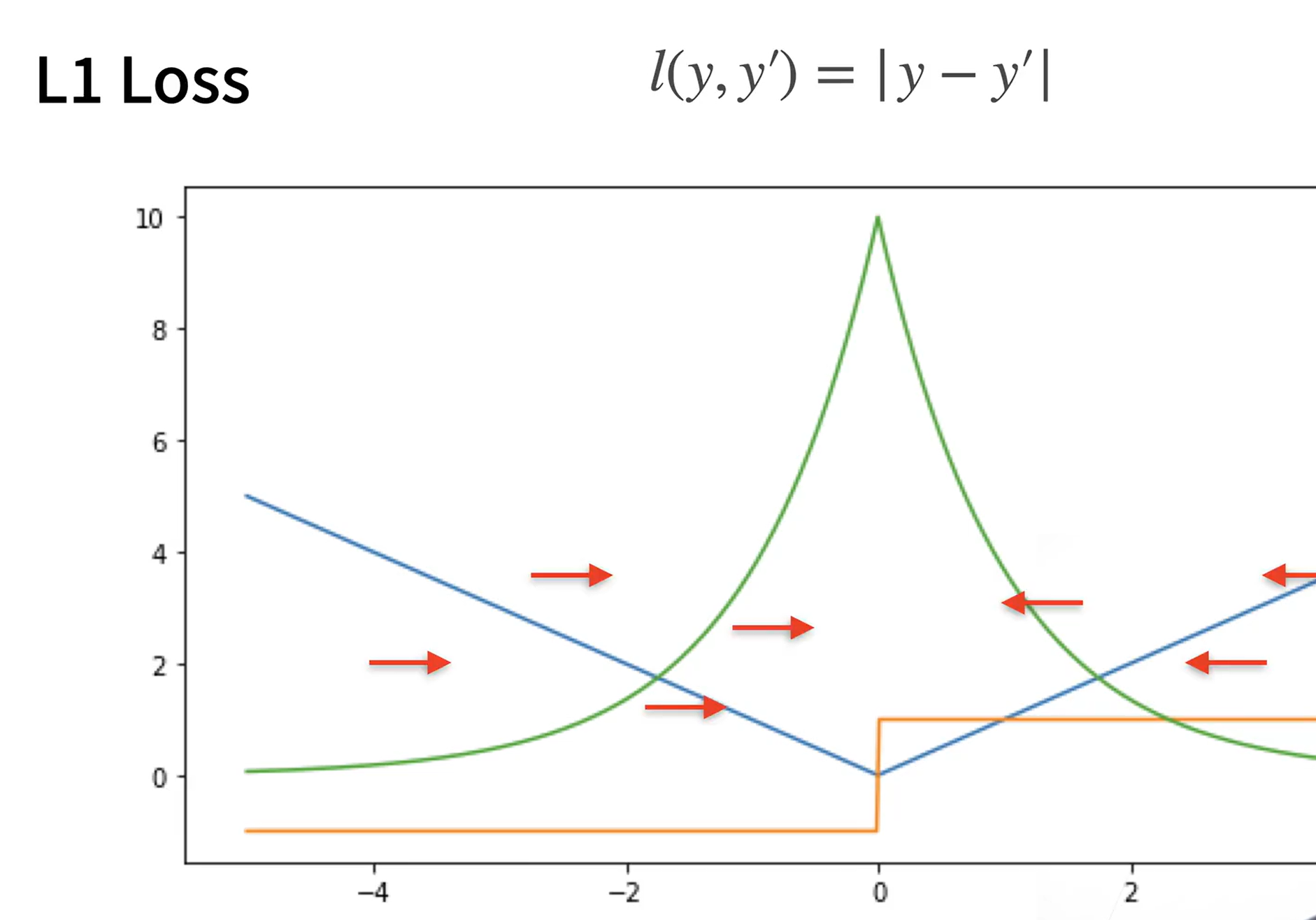
缺点:原点处不可导;y’和y离得很近的时候不稳定 -》结合L1和L2 Loss得到下面这个损失函数
Huber’s Robust Loss
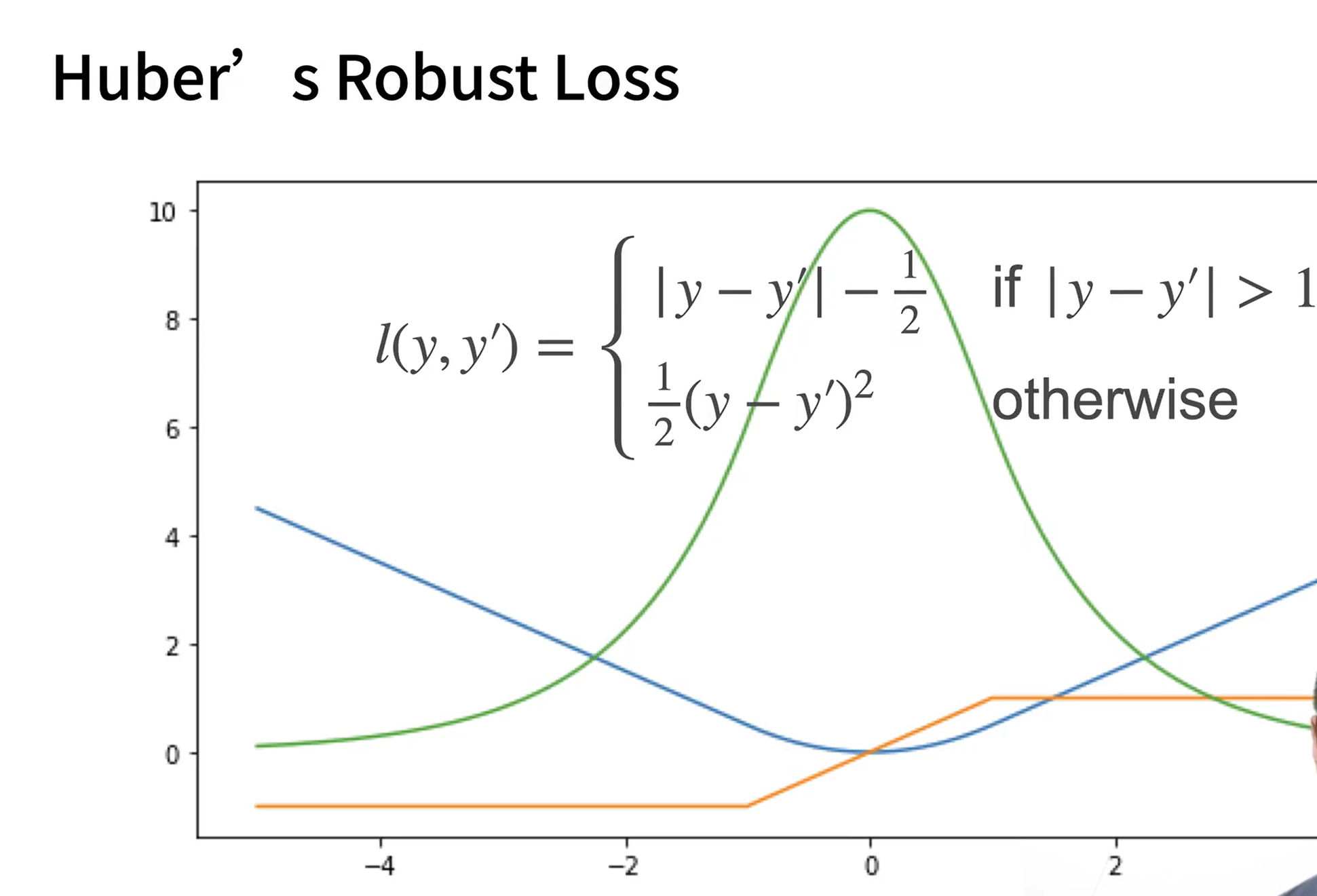
鲁棒性 robustness
系统的健壮性——系统在特殊情况下的稳定性
四、感知机
感知机

只输出一个离散的类,因此只能用于二分类
- 最早的AI模型之一
- 求解算法等价于使用批量大小为1的梯度下降
- 不能拟合XOR函数
多层感知机 MLP(Multilayer Perceptron)
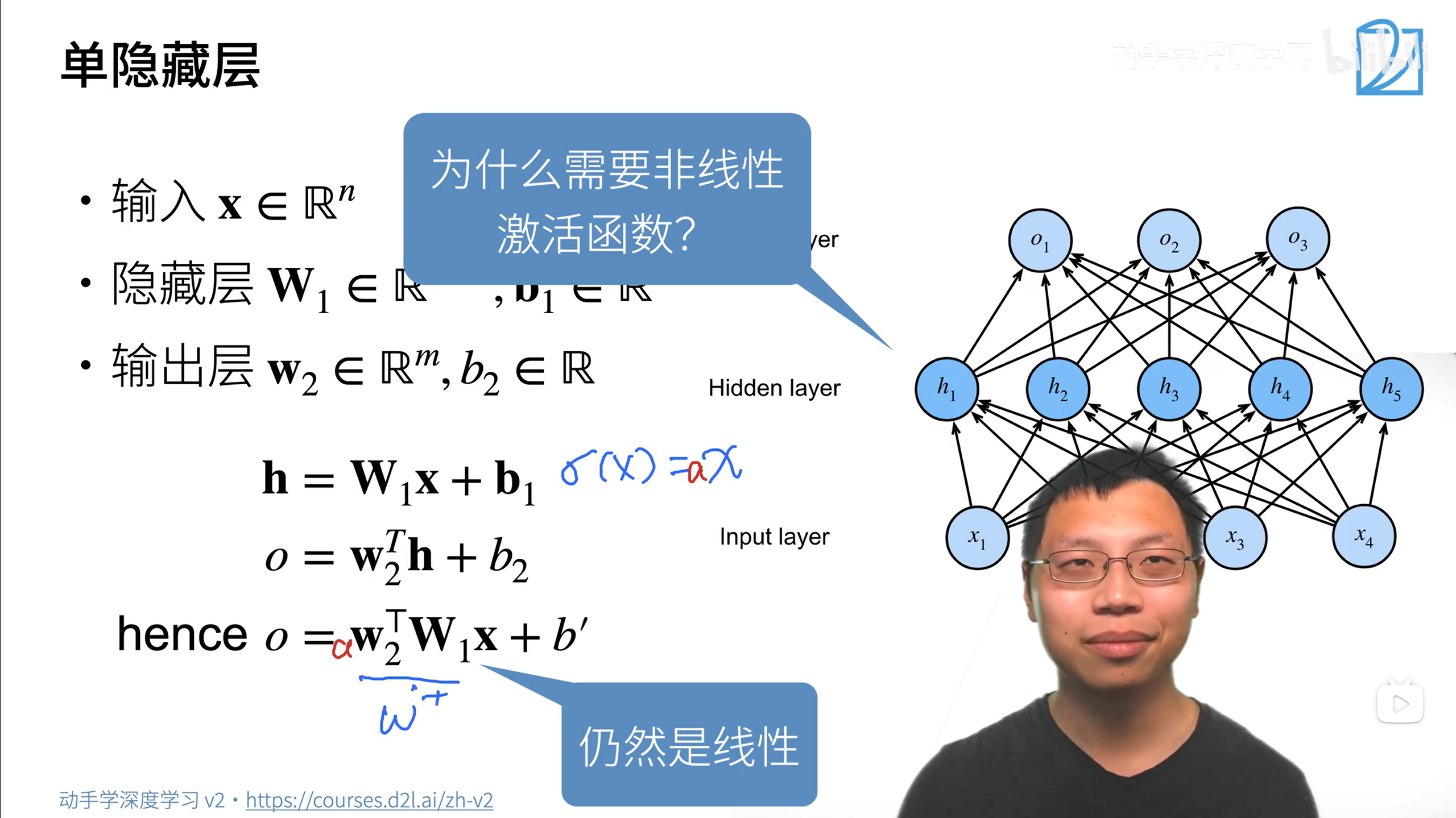
这样得到的结果还是线性的,和单一的线性模型没什么区别(只是加权偏移,限制了对复杂任务的处理能力,只能解决线性问题),因此需要加入非线性激活函数
神经网络为什么working?
将同一个输入给不同的神经元,每个神经元学习不同的特性,在最后线性计算合并这些特性,输出结果。
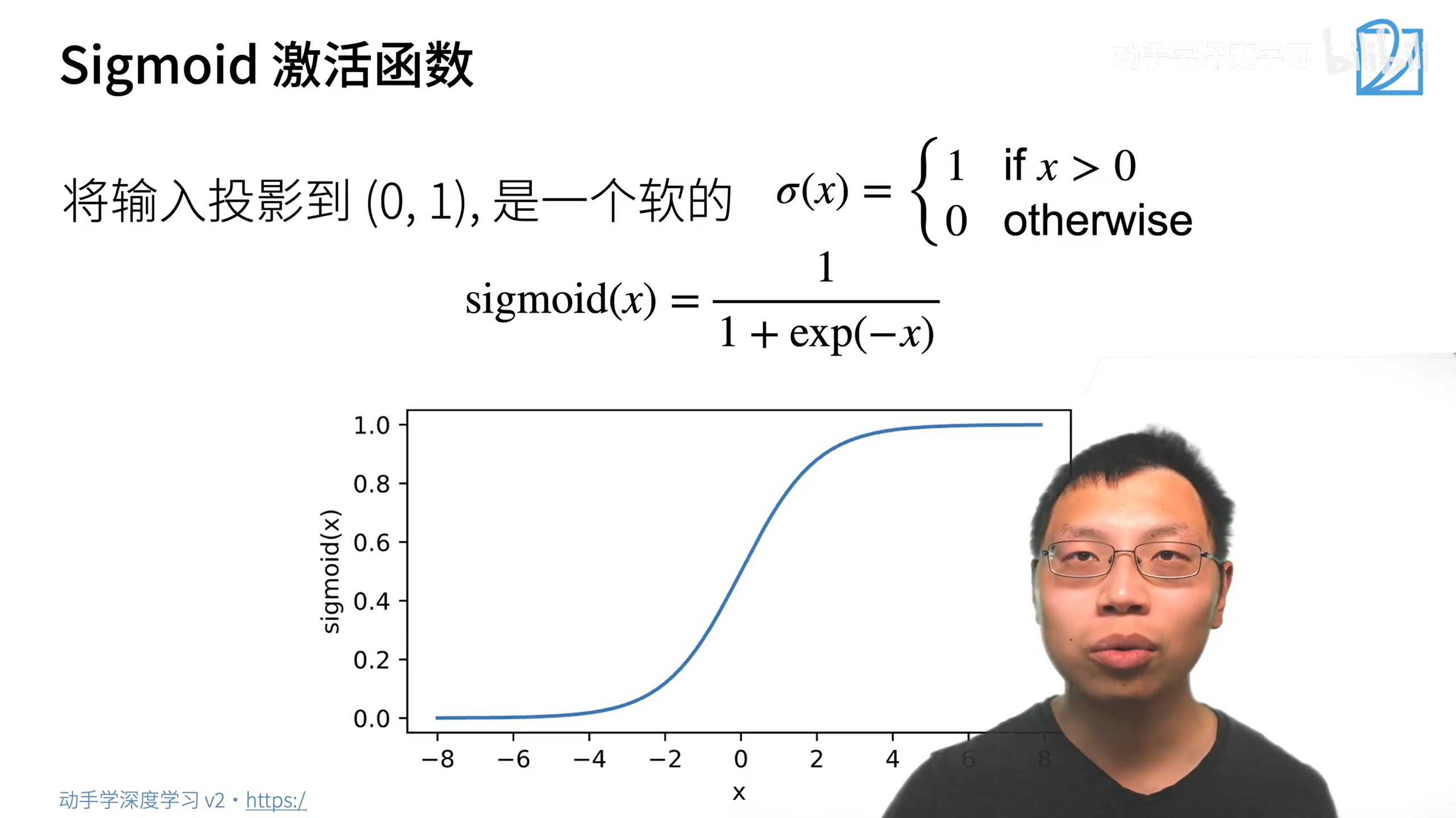
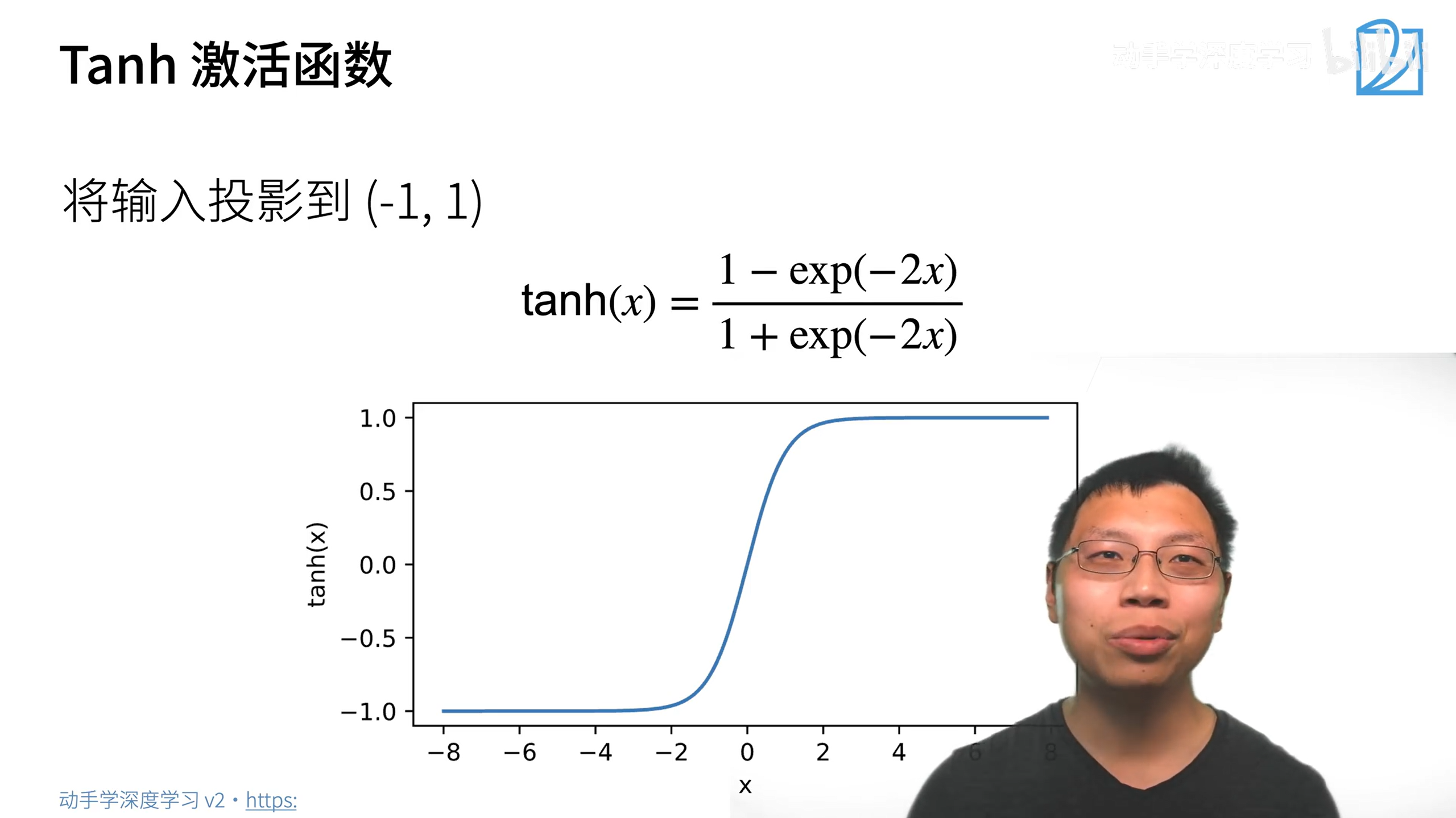
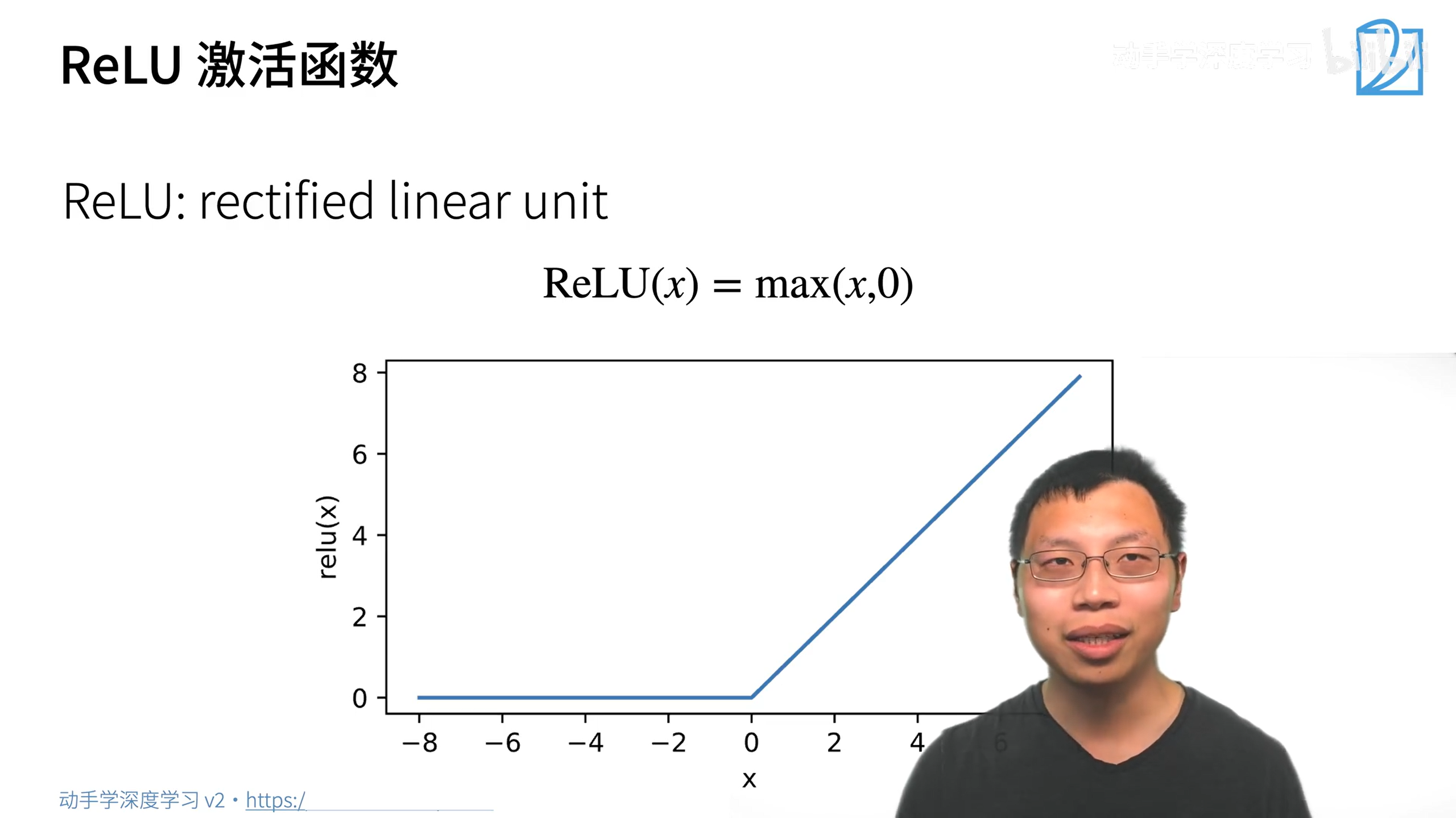
非线性激活函数
激活函数的本质就是引入非线性性
用relu就好了,用其他的区别也不大。而且relu计算更快
nn.ReLU(inplace=True)中的inplace表示直接原地修改内容,而不是新开内存进行修改,可以节省一点内存。
多隐藏层
多隐藏层一般是先扩展再压缩,先压缩的话会损失很多信息。
最后一层不要加非线性激活函数,加了会造成层数的塌陷。
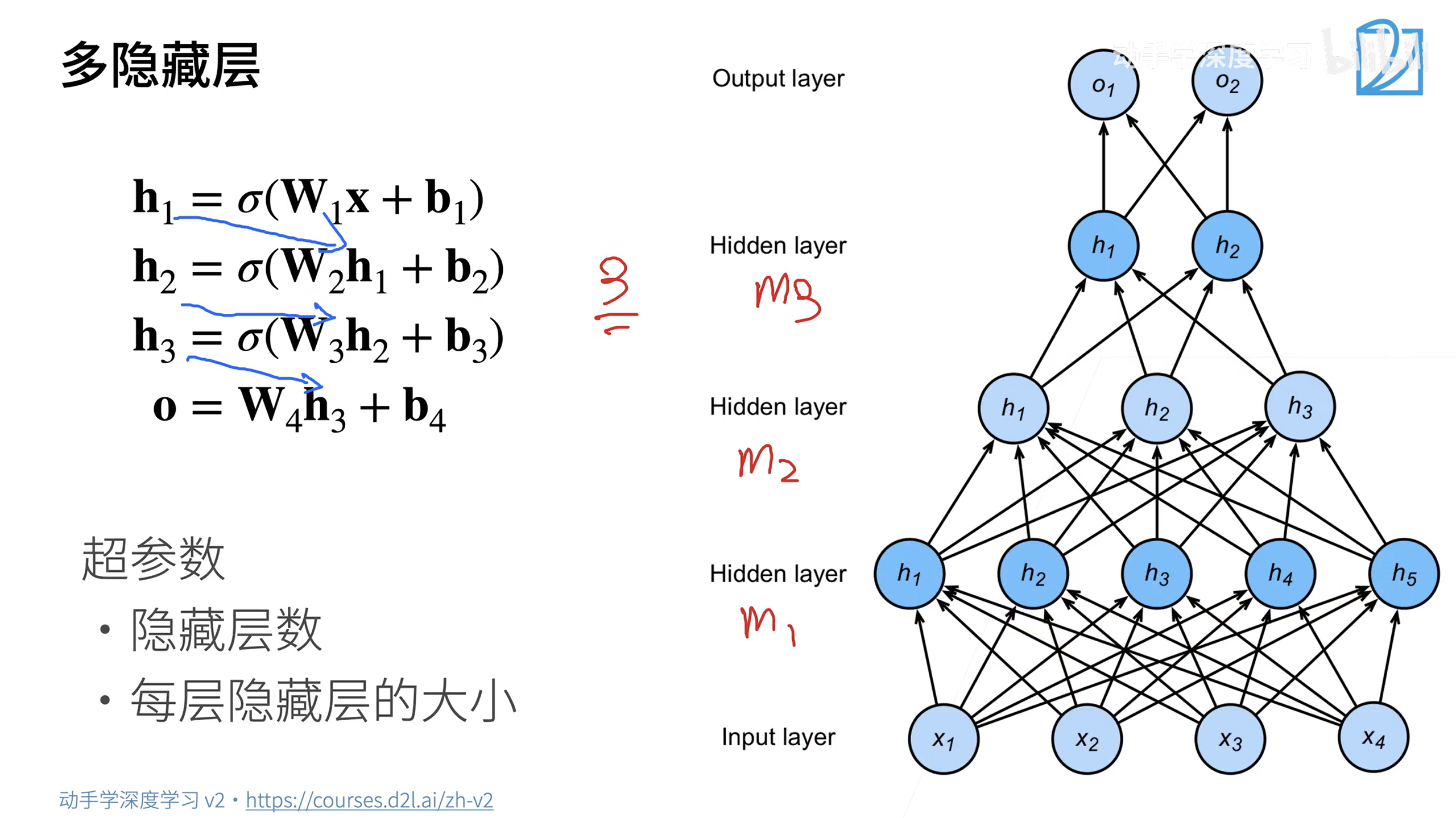
为什么是多层而不是一层很宽?
一层很宽,即让很多神经元在一起学习,不一定会有很好的效果,可能会导致过拟合。而多层的话相当于一次学一点。—>深度学习
五、模型选择
训练误差、泛化误差
训练误差:模型在训练数据上的误差
泛化误差:模型在新数据上的误差
验证数据集、测试数据集
验证数据集:一个用来评估模型好坏的数据集
- 例如拿出50%的训练数据
- 不要跟训练数据混在一起!!
测试数据集:只用一次的数据集
例如:
- 未来的考试
- 房子的实际成交价
K-则交叉验证
在没有足够多数据时使用
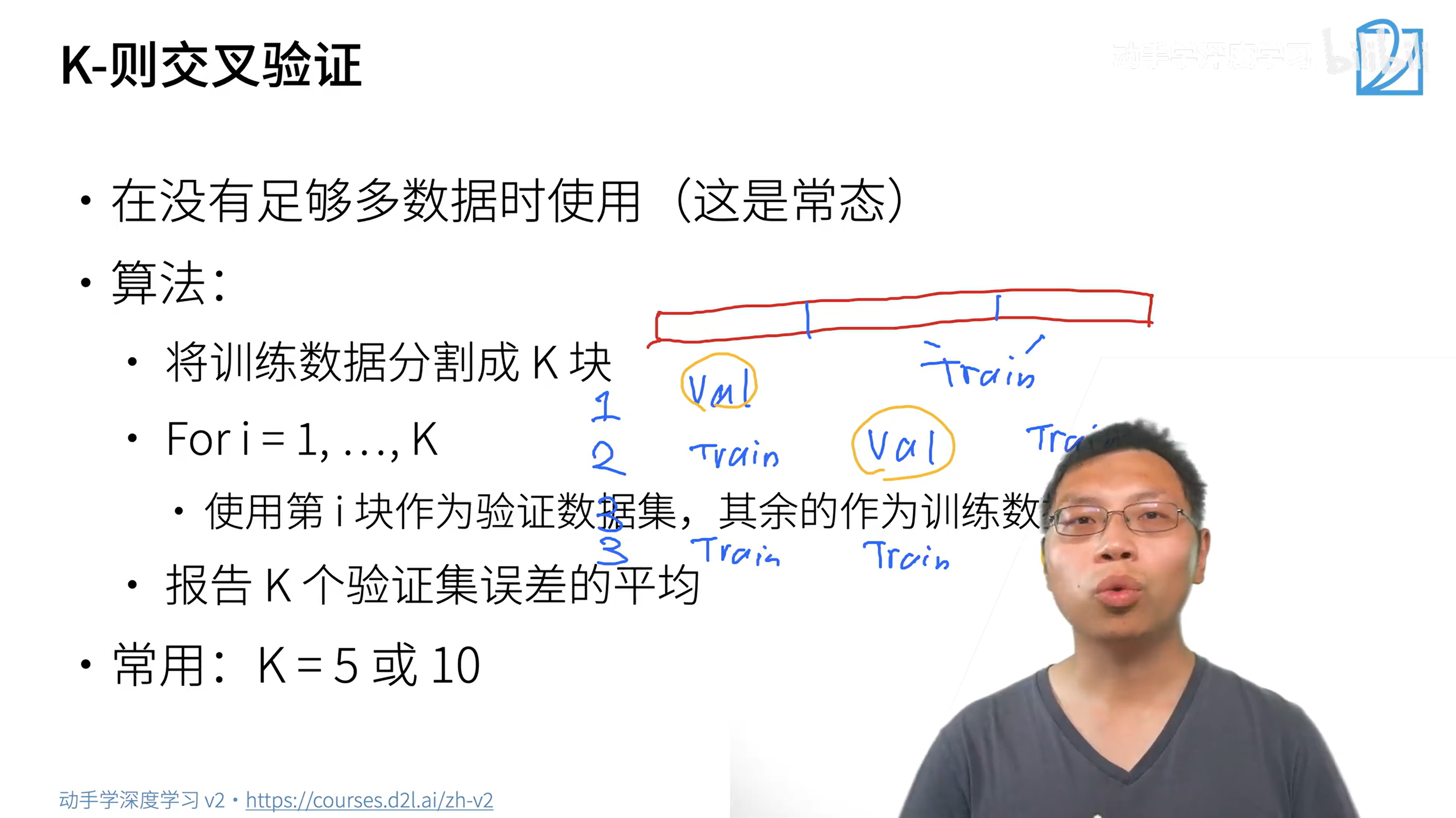
最后选择最好的那一次的参数作为模型的参数
过拟合、欠拟合
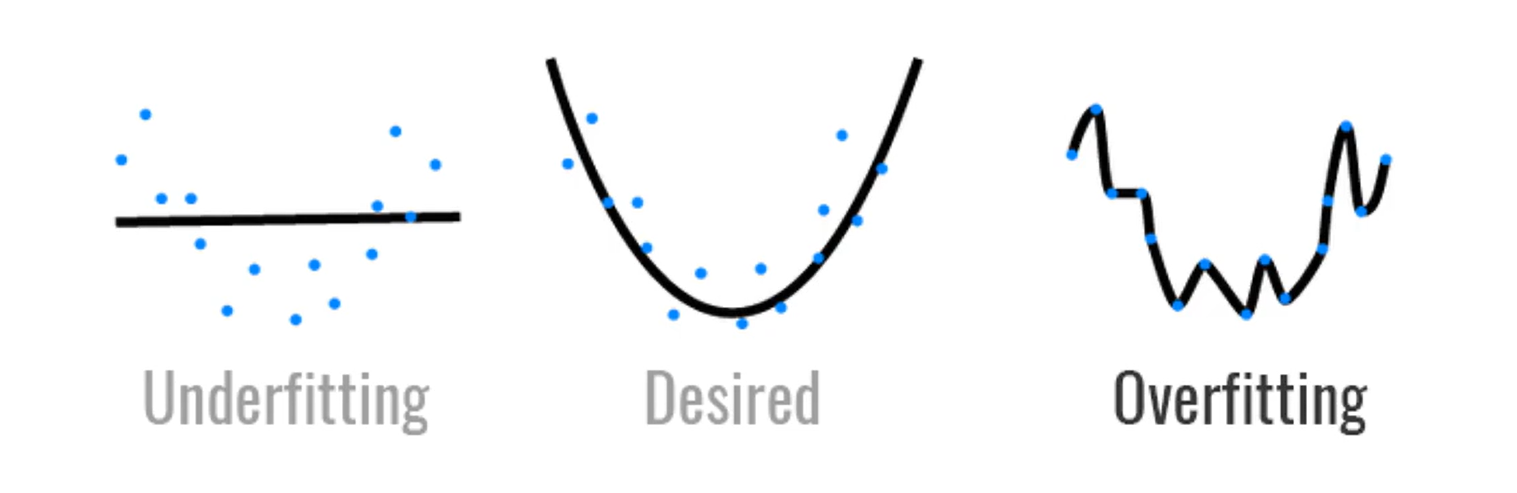

过拟合:数据很简单,模型容量很高,模型可能记住这些数据,但别的数据拟合程度不高。
模型容量
拟合各种函数的能力
- 低容量的模型难以拟合训练数据
- 高容量的模型可以记住所有的训练数据
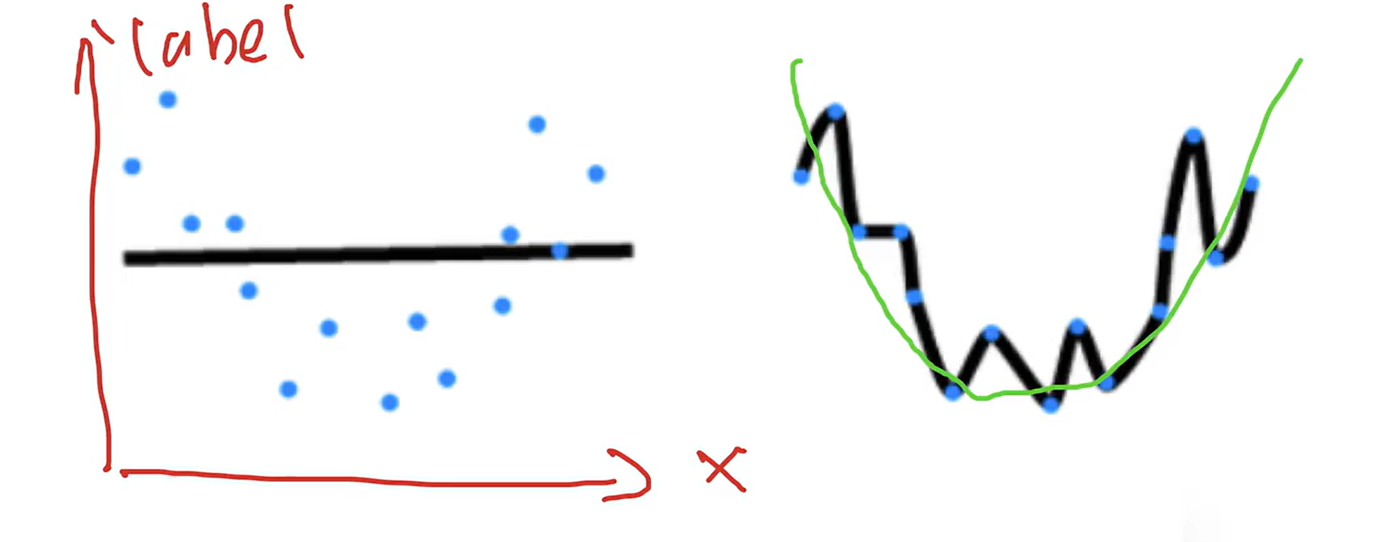
首先模型要大,再考虑怎么降低泛化误差
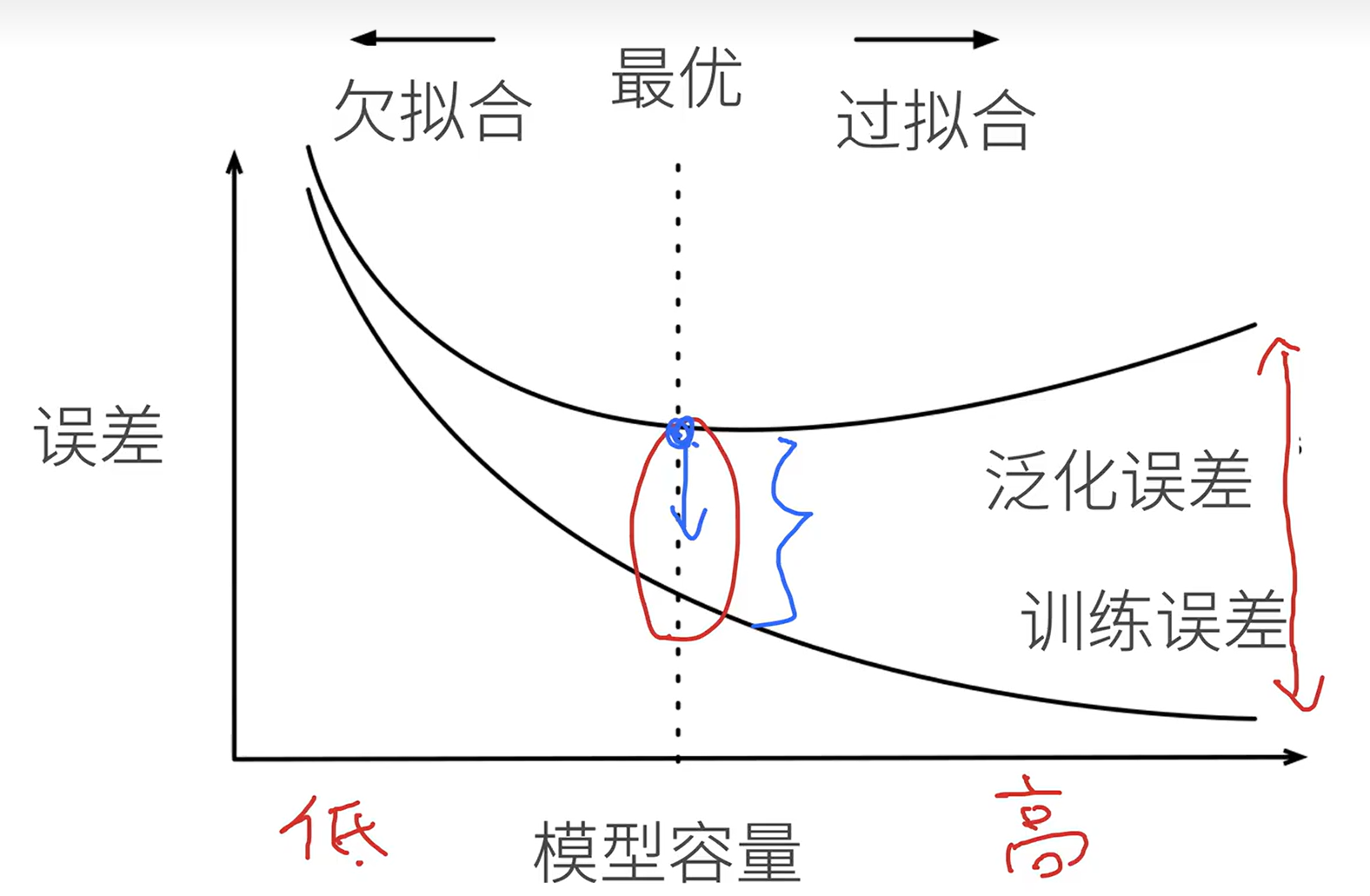
估计模型容量
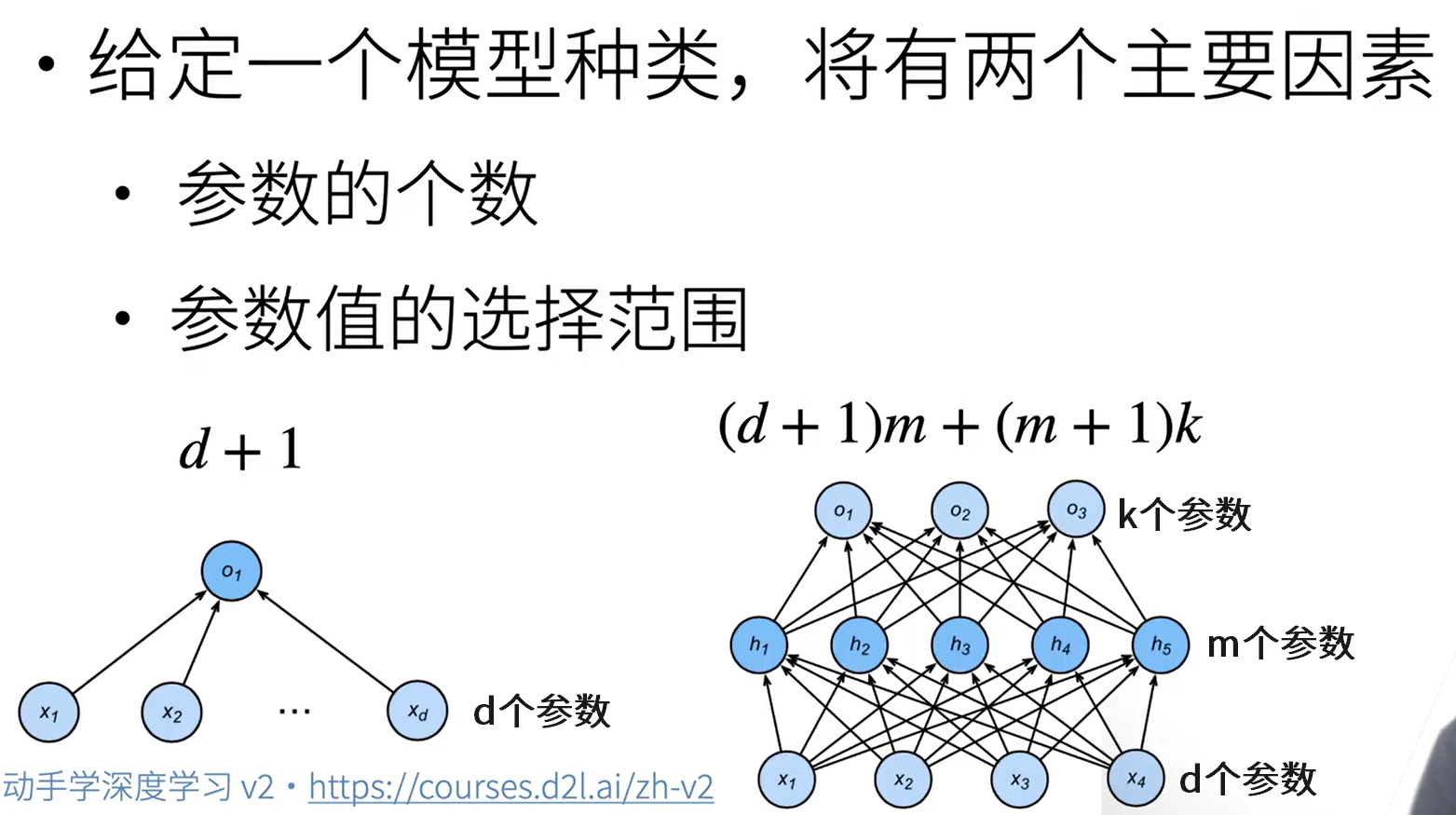
数据复杂度
- 样本个数
- 每个样本的元素个数
- 时间、空间结构
- 多样性
六、权重衰退
范数
高维空间中一点到原点的距离
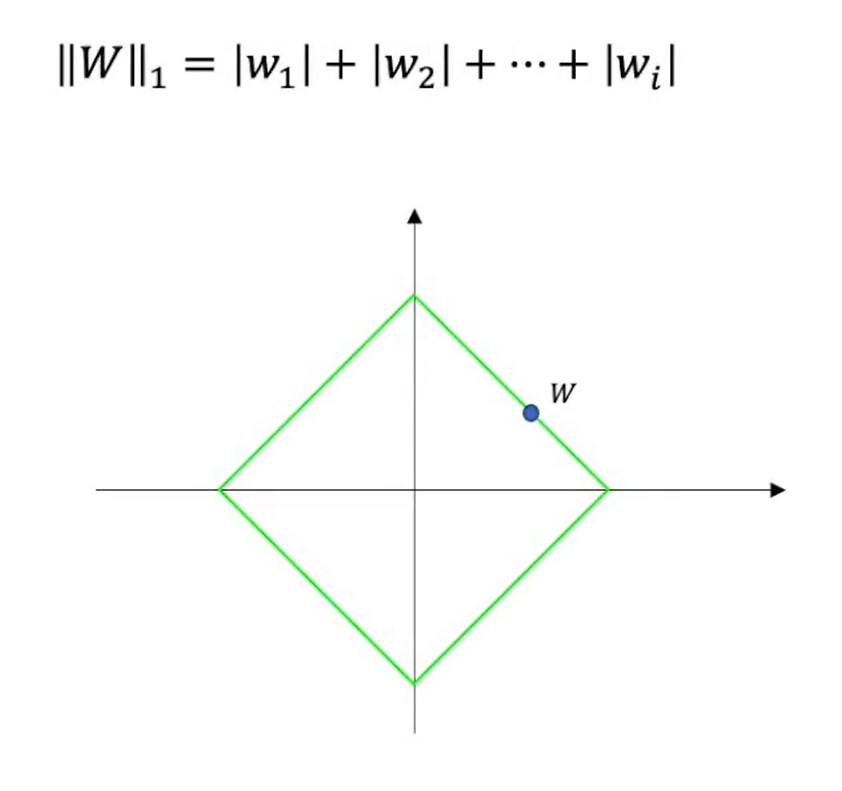
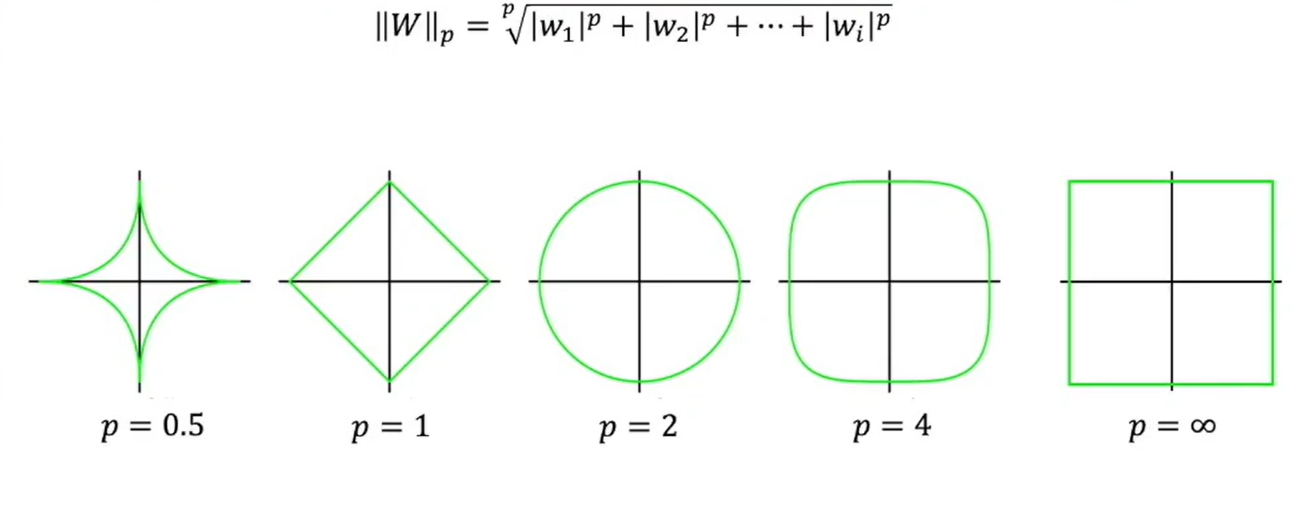
L1范数 —— 曼哈顿距离
各坐标值绝对值相加
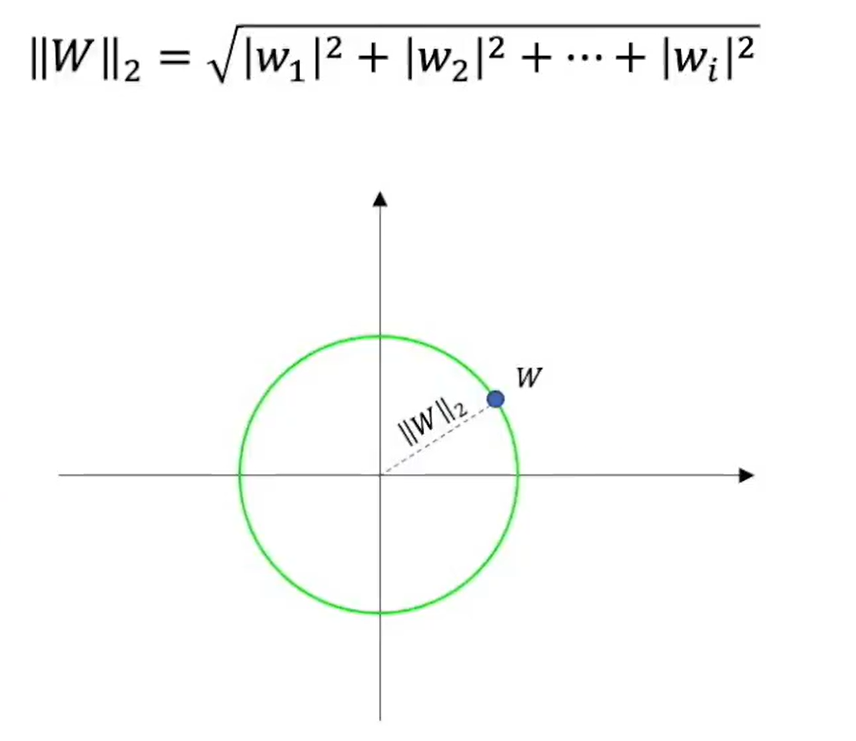
L2范数 —— 欧几里得距离
高维中的勾股定理
LP范数
正则化 —— 权重衰退
每一次会缩小w的取值范围
如果模型很复杂,权重衰退也不会带来很好的效果。
为什么需要正则化?
模型可能会过度拟合训练数据,过于依赖训练数据中的噪声和细节。正则化通过降低模型的复杂度来防止过度拟合。
正则化会在损失函数中加入一个正则化项,它会使模型中的某些参数不能太大,因此模型会更倾向于选择那些对预测结果有更大影响的参数,减少对其他参数的依赖。

L1正则化
L1正则化可能带来稀疏性,某些特征就不起作用了(去耦合,减少过拟合)
L2正则化
只缩小了W的权重
如何操作
1、手动
如果是手动加的话,就是在loss函数中加一个正则化的式子
λ自己试,看看什么时候好
2、在trainer中加参数
加一个weight_decay的参数,一般设置成1e-3

这里使用的是L2范数的平方
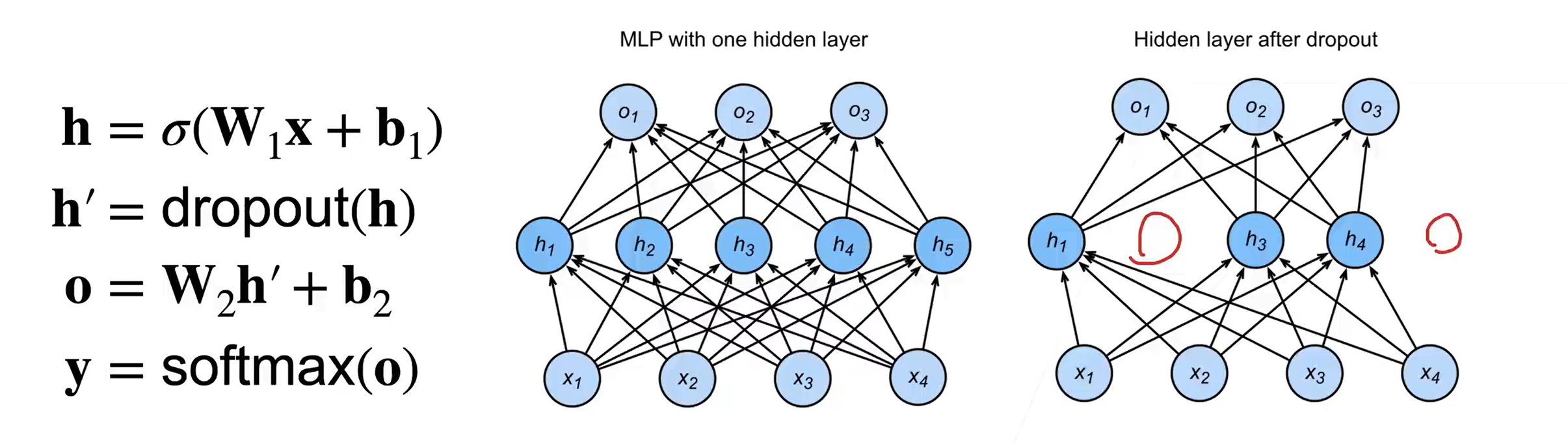
七、丢弃法 dropout
在层之间加噪音
只在训练中使用,在预测中不使用。在测试时,Dropout层仅传递数据
动机
一个好的模型需要对输入数据的扰动鲁棒robust
无偏差的加入噪音

一定概率变成0,一定概率x值变大,但期望不变
使用丢弃法
通常将丢弃法作用在隐藏全连接层的输出上
全连接层——每一个结点都与上一层的所有结点相连
八、数值稳定性
数值爆炸
值超出值域,对于16位浮点数尤为严重
对学习率敏感
如果学习率太大->参数值会大->更大的梯度
如果学习率太小->训练无法进展
需要再训练中不断调整学习率
梯度消失
- 梯度值变成0
- 对16位浮点数尤为严重
- 训练无进展
- 对底部层尤为严重
- 仅仅顶部层训练的较好
- 无法让神经网络更深
让训练更稳定

合理的权重初始值和激活函数的选取可以提升数值稳定性
每一层的输出E=0,D=一个常数
九、kaggle 房价预测
标准化
数据预处理
标准化数据
